


The novel presents 1467 characters, from detectives to race car drivers, merchants, housewives, actors, scientists, craftsmen, martial artists, writers, painters, explorers, and people from every conceivable walk of life, capturing an incredibly diverse range of narrative tones produce endless combinations of places, things, and events. Even these combos are not left to chance.
Perec wishes to regulate them by following a strict protocol, which adds another level of complexity to the rooms'/chapters' rigid and articulated structure. That’s when he created a Cahier des Charges, lists of items organized by ten and attributed to twenty-one pairs of categories. The creation alone took Perec two years.
The categories are:
- position – activity;
- quote 1 – quote 2;
- number – role;
- 3rd sector – actions;
- walls – floors;
- epoch – place;
- style – furnishings;
- length – different;
- age and sex – animals;
- clothes – fabrics (type);
- fabrics (materials) – colors;
- accessories – jewelry;
- readings – music;
- paintings – books;
- drinks – foods;
- small furnishings – games and toys;
- feelings – paintings;
- surfaces – volumes;
- flowers – ornaments;
- absence – false;
- couple 1 – couple2
Some of these may be linked back to tangible things, while others stay abstract, and others condition the unfolding of events (as in the actions category) or narrative style (as in the 3rd sector with food recipes or technical manuals), or even the size of the chapter.
Categories of absence and fake are also present, allowing the violation of some rules (a different way to insert clìnamen). Moreover, each category has 10 arbitrary items.
Here's the full grid.
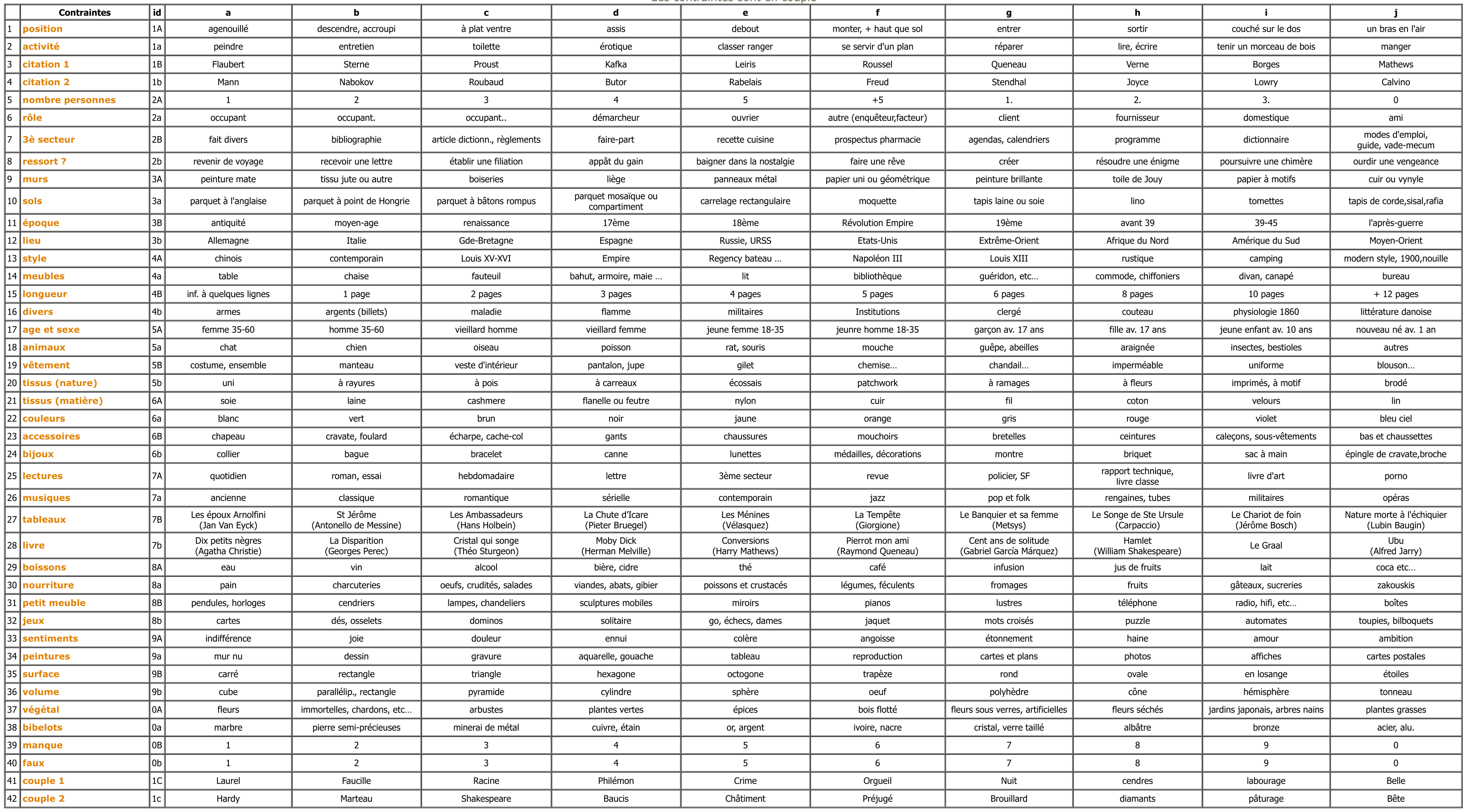
Click on the image to zoom it and navigate its content.
Perec joined each of the ten components from the first category with the ten elements from the second to generate 100 distinct pairs of elements for each couple of categories. For instance, all ten of the items in category 8a, "foods," such as "bread, meat, eggs, crudité, salads, etc.," will be paired with the first item in category 8A, "drinks," which is "water"; the same goes for the second, third, and so on.
When Perec repeats the process for each of the 20 couples (apart from the manque/faux pair), 2000 distinct combinations result. These combinations were placed in grids identical to those used for the Polygraphie du Cavalier and the design of the building's portion. Perec substitutes the verbal categories listed in Cahier des Charges with the relevant numbers to create the grids (from 0 to 9).
The author additionally employs a second tool, a Double Latin Square based 10: a chessboard with ten rows and ten columns and two integers from 0 to 9 set in each cell, to rigorously identify the elements (one placed at the top left and one lower right).
The regular Latin Square is a chessboard with a different number in each square set up so that each digit only occurs once in each row and column, but in Perec’s grids, each of the 100 boxes in the 10x10 square has two numbers (Double Latin Square). These numbers represent the values of the linked categories and only one instance of each pair must be present in each row and column of that arrangement.
As a result, there were 20 double latin squares, one for each pair of categories. Perec could then plot the narration by using the numbers in each square (room/chapter) to select the components from the lists without repeating or omitting anything.
Using twenty separate Double Latin Squares, components with the same numbers might occur in the same chapter, even if connected to pairs of different categories, therefore Perec rejected this alternative and created 20 Double Latin Squares without repeating pairings of integers in the same cell - another tailored exception.
We will not go into details about the complexity of the quenine, which also includes some other constraints introduced and never explained by Perec.
As we are going to see, we will not need it to run the machine.


2022, Diego Chillo & Laura Travaglini